Pinning Down Arc Consistency 3

If you've read up on my Wave Function Collapse (WFC) misadventures, you'll notice I discuss the Arc Consistency algorithm in the intermission. I wanted to create a system that required slotting colored marbles into spaces on a pattern that enforced relationships between the colors of the marbles.

This took me to the Arc Consistency (AC-3) algorithm. It described everything I wanted:

• A set of variables with specified domains
• A set of single-sided or double-sided restrictions
• A known runtime complexity of $O(e{d}^3)$ where $e$ is the number of edges, and $d$ is the largest domain size.

Since I was too WFC-pilled at the time, I ended up not pausing my work on the colored marble system and pivoting back to my rectangular grids. I was able to implement AC-3 so that it drove a Wave Function Collapse level generator. I got it to the point where it'd stop at contradictions. Backtracking would be a problem for future me.

Well, I'm future me and now I have a problem.

I want something very specific, and by specific, I mean extremely general. My goal is to create an Arc Consistency 3 graph that:

• Is Lightweight: The previous implementations I've written involved large classes for both the nodes and the arcs. I refuse to have this be the case again.
• Is Fast...er: Getting AC-3 to be faster is going to be rough. (I am learning AC-4 exists while I'm writing this. So, uh, after reading up on it and looking at the space complexities, I've decided to hold back on upgrading to AC-4 right this moment.) At least when it comes to AC-3, the most I can do is minimize overhead from excessive use of weird data structures.
• Is General Purpose: I'm talking:
  • Generic Classes so the nodes can be of any type. They're not getting stored in the graph anyway, so...
  • Delegates for the constraints. Instead of storing constraint functions in the implementation, I want the constraint functions to be provided to the constructor of the graph instead.
• Is Clean to some degree. If I want this to be used by people, I need to make sure it's easy to use.

The Plan

Here is the UML diagram I decided to go with for my data:

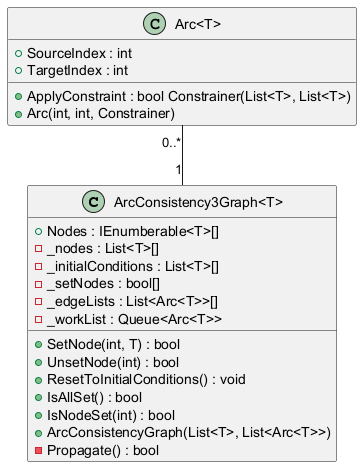
Unlike previous implementations, nodes are no longer classes. Instead they are just lists of their possible values. Those lists are stored in an array _nodes. However, since the user might want to see what's inside a node, the nodes are made visible through the Nodes property which returns _nodes as an IEnumerable so the nodes can't be edited from outside the class.

The graph itself would be implemented as an array of edge lists. Each element of the array is a list of edges coming out of the node at that index. In this case, I'm using an Arc class to store the edge data. Providing the arcs as lists of sources, targets, and constrainers wasn't clean enough enough for me. I needed to group those elements together to make it easier to pass that data to the constructor of the graph. Thankfully the Arc class itself wasn't too heavy.

The Implementation

Let's start with the Arc class. Pretty simple. Just two ints and delegate:

public class Arc<T> {
    public delegate bool Constrainer(List<T> sourceList, List<T> targetList);

    public int SourceIndex {get; private set;}
    public int TargetIndex {get; private set;}
    public Constrainer ApplyConstrainer {get; private set;}

    public Arc(int sourceIndex, int targetIndex, Constrainer constrainer) {
      SourceIndex = sourceIndex;
      TargetIndex = targetIndex;
      ApplyConstrainer = constrainer;  
    }
  }

The delegate here is being used to outsource the arc's constraint logic. Previously, I had embedded arc constraint logic into the arcs themselves. This time I decided to go against that just because it means the arc class can be as general purpose as possible. I could've opted for an interface or abstract class, but I wanted to make it easier on the user to work with. After all, the indices should still work the same, it was just the restraint logic that needed to change.

Now that the Arc class was ready, it was time for the magic to happen:

public ArcConsistency3Graph(List<T>[] nodes, List<Arc<T>> arcs) {
  _initialConditions = nodes;
  // Convert arc list into edge list
  _edgeLists = new List<Arc<T>>[_initialConditions.Length];
  for(int i = 0; i < _initialConditions.Length; i++) {
	_edgeLists[i] = new List<Arc<T>>();
  }
  foreach(var arc in arcs) {
	_edgeLists[arc.SourceIndex].Add(arc);
  }

  _nodes = new List<T>[_initialConditions.Length];
  _setNodes = new bool[_nodes.Length];
  _workList = new Queue<Arc<T>>();
  ResetToInitialConditions();
}
    
public void ResetToInitialConditions() {
  for (int i = 0; i < _nodes.Length; i++) {
	_nodes[i] = new List<T>(_initialConditions[i]);
	_setNodes[i] = false;
	foreach(var edge in _edgeLists[i]) {
	  _workList.Enqueue(edge);
	}
  }
  if(!Propagate()) {
	throw new InvalidOperationException("Initial arc conditions result in a contradiction.");
  }
}

The constructor takes in a list of nodes (in their initial conditions) and sets those to the _initialConditions variable. It then converts a list of Arcs into an edgelist. After that, it calls the ResetToInitialConditions() function, which creates a copy of each initial condition into its node, sets their setNode value to false (signifying the node hasn't been set), and queueing up all the arcs in the graph for propagation. It then propagates all changes. If this initial propagation results in a contradiction, the graph will throw an error, stating that the provided nodes and arcs cannot be used.

The next bit of magic happens in the Propagate() function which should return false if there was a contradiction found, and true otherwise. This is just the C# version of the pseudocode on the algorithm's Wikipedia page:

private bool Propagate() {
  while (_workList.Count > 0) {
	Arc<T> arc = _workList.Dequeue();

	if(arc.ApplyConstrainer(_nodes[arc.SourceIndex], _nodes[arc.TargetIndex])) {
	  // A change was made upon application of the rule.
	  if(_nodes[arc.TargetIndex].Count == 0) {
		_workList.Clear();
		return false; // Contradiction
	  }
	  // Queue up arcs coming from target
	  foreach(var outGoingArc in _edgeLists[arc.TargetIndex]) {
		if(outGoingArc.SourceIndex != arc.SourceIndex) {
		  _workList.Enqueue(outGoingArc);
		}
	  }
	}
  }
  return true; // No contradictions
}

The only thing to note here is the ApplyConstrainer() function being called from the arcs should return true if there was a change made to the target list and false otherwise. If a change is made to the target, its outgoing arcs are all queued up except for the one that goes to the node that just propagated to it.

After this, it was just a matter of writing the SetNode() and UnsetNode() functions.

public bool SetNode(int nodeIndex, T nodeValue) {
  // Returns false if there is a contradiction, otherwise true.
  if(_setNodes[nodeIndex])
  {
	throw new InvalidOperationException($"Node {nodeIndex} already set.");
  }
  if(!_nodes[nodeIndex].Contains(nodeValue)) {
	throw new InvalidOperationException($"{nodeValue} is not a possible choice for Node {nodeIndex}");
  }
  _setNodes[nodeIndex] = true;
  _nodes[nodeIndex].Clear();
  _nodes[nodeIndex].Add(nodeValue);

  foreach(var arc in _edgeLists[nodeIndex]) {
	_workList.Enqueue(arc);
  }

  return Propagate();
}

Nothing out of the ordinary here. Just error checking and then setting the node. When a node is set, it is cleared of all of its possible values and only given the value it was set to. Then all its outgoing arcs are enqueued into the worklist and propagated. If a contradiction is found, the class returns false, otherwise true.

As for the UnsetNode() function, I unfortunately couldn't find a way to propagate the changes without nuking the rest of the unset nodes back to their initial states and then propagating all arcs except the ones to set nodes.

public bool UnsetNode(int nodeIndex) {
  if(!_setNodes[nodeIndex]) {
	throw new InvalidOperationException($"Node {nodeIndex} not set.");
  }
  
  _setNodes[nodeIndex] = false;

  for(int i = 0; i < _nodes.Length; i++) {
	if(!_setNodes[i]) {
	  _nodes[i] = new List<T>(_initialConditions[i]);
	}
	foreach(var arc in _edgeLists[i]) {
	  if(!_setNodes[arc.TargetIndex]) {
		_workList.Enqueue(arc);
	  }
	}
  }

  return Propagate();
}

Of course, we do a little bit of error checking to make sure the node we want to unset has already been set. We then set it's _setNodes flag to false. We reset all the unset nodes and add their outgoing arcs to the list (except for those that lead to a set node) and propagate, returning false if a contradiction is found, true otherwise.

That's basically it. After that, I just added two funny little guys for more information the user might want because exposing the _setNodes array isn't a good idea, imo.

public bool IsAllSet() {
  foreach(var setValue in _setNodes) {
	if(!setValue) return false;
  }
  return true;
}

public bool IsNodeSet(int nodeIndex) {
  return _setNodes[nodeIndex];
}

This should provide the user with the information necessary when running an automatic solver, like this one algorithm I've heard of called Wave Function Collapse??? Maybe you've heard of it??? I don't know. I've only vaguely heard the name.

Evaluation

What I like about this class is it's genuinely pretty lightweight, fast, and yet really versatile. I ran it on a graph of ints that forced relationships between them like less than, greater than, equality, inequality, parity equality, and parity inequality. The tests ran pretty well. But for a more fun test, I ran it on the Queens puzzle and look at this beauty:

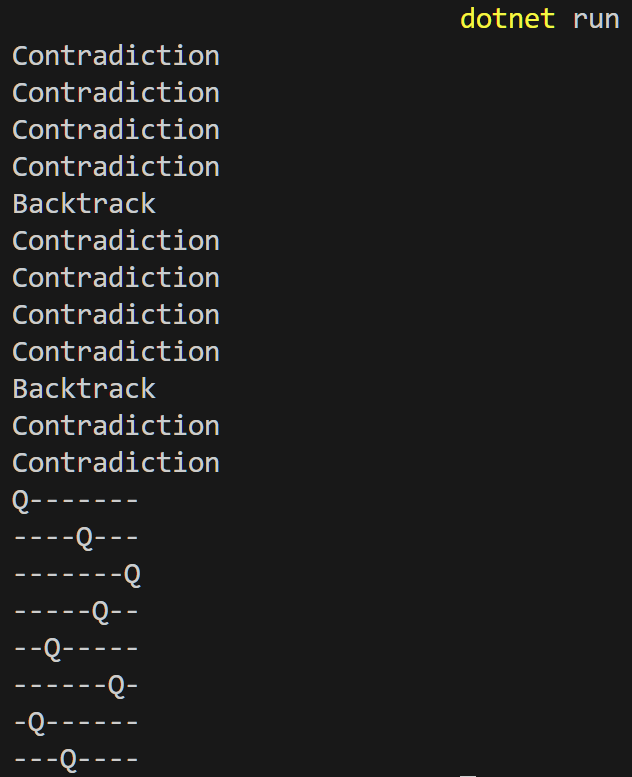
You see that magic word there? It starts with a "B." That's right! Backtracking works! And it wasn't a part of the actual ArcConsistency3Graph class, but it wasn't difficult to implement with a stack. After all the actual graph can't have its own backtracking logic, because that logic depends on the selection algorithm. For the queens puzzle it wasn't too hard to implement. It was just making it move onto the next tile that might work in that row.

You can check the algorithm out in the tests folder of the project's Github repository.

If you've read my Wave Function Collapse journey, you'll remember that the algorithm uses an entropy heuristic to select the next node to collapse, along with a weighted random selection to select the element to collapse to. This arc consistency implementation outsources all selection logic, making the data structure separate from the node-setting behavior. I could take the graph I use in WFC and instead let it use manual user input instead to set nodes. It would still propagate constraints the exact same way, and I wouldn't need to worry about coding that propagation logic anymore.

Speaking of WFC, now that I've got backtracking implemented with this graph, I'm really looking forward to going back and implementing backtracking in WFC. Hopefully this graph will make things less painful.

Stay tuned for that blog post!